Haskellで数値計算

普段はJavaやFortranで数値計算をしているのだが、使える範囲でHaskellも使ってみたくなった。宣言的に書けるのでコードが簡潔になることや、副作用が厳格に管理されている上に、静的な型付けがしっかりしていてコンパイラが賢いので、バグが見つけやすいことなどがうれしい。ただ、自分で管理できるワークステーションならともかく、スパコンにGHCを入れて多次元の流体計算などしたいとなると、どうだろうか。Fortranよりも計算資源を効率的に使えていると説明できないといけないかもしれない。一方で、MathematicaやPythonでやっているような計算の一部は、Haskellでより柔軟に速くできることも多そうだ。ここでは、よく使われる簡単なアルゴリズムを書いてみた。

目次

準備と方針

処理系はGHC 8.0.2を使っている。また、行列計算のためにhmatrixパッケージを入れた。(ここではcabalを直接使っていますが、状況に応じてStackなどを使ってください。) 行列分解や連立線形方程式を解くアルゴリズムもいずれ紹介してみたい。

> cabal update
> cabal install hmatrix

ここでは、そこまで速度やメモリにシビアではない状況を考えている。速度やメモリを気にする場合は、リストの代わりにData.Vector.UnboxedのVector (参照ではなく値の配列で、要素を辿るようなライブラリ関数はFusionが単一のループにしてくれたりするらしい) を使ったりすると良い。使い勝手もリストとそれほど変わらない。
Numeric Haskell: A Vector Tutorial - HaskellWiki
vectorパッケージはhmatrixを入れると付いてくる気がするが、個別にインストールすることもできる。

> cabal update
> cabal install vector

また、アルゴリズムの選択は何より性能に影響をあたえると思うが、ここでは見通しを優先して逆行列を計算するライブラリ関数を素直に使っていたりするので、その辺りは必要に応じて適宜修正してほしい。hmatrixの逆行列関数はLU分解で逆行列を計算しているので、1000 1000程度までの行列を数十回計算する程度なら問題なさそうではある。並列計算についてもそのうち紹介してみたい。

4段4次の古典的Runge-Kutta法

まずは連立常微分方程式 (ODE) を解いてみる。4段4次の古典的Runge-Kutta法は簡単で精度や速度もそれなりなので、よく使われている。ただ陽解法なので、問題によっては適さないこともある。その場合、hを小さくしたり可変にしたりしてみて、それでもだめなら、ステップごとに非線形方程式を解くことになるが、1段2次から3段6次程度までの陰的Runge-Kutta法なども使えるかもしれない。

import Data.List (zipWith5)

rungekutta_44 :: [[Double] -> Double] -> Double -> Double -> [Double] -> IO ()
rungekutta_44 dfs h lim ps@(t:xs) = do
  print ps
  if t > lim then return ()
  else rungekutta_44 dfs h lim ((t + h):ss)
    where k1s = map ($ ps) dfs
          k2s = kf 0.5 0.5 k1s
          k3s = kf 0.5 0.5 k2s
          k4s = kf 1.0 1.0 k3s
          kf tc xc ks = map ($ (t + tc*h):zipWith (\x k -> x + xc*h*k) xs ks) dfs
          ss = zipWith5 sx xs k1s k2s k3s k4s
          sx x k1 k2 k3 k4 = x + (h/6.0)*(k1 + 2.0*k2 + 2.0*k3 + k4)

高階微分の方程式を解く場合、新しい変数を導入して1階微分の方程式を連立させることになるので、これを自動化してくれる関数も書いてみた。

rungekutta_44_s :: ([Double] -> Double) -> Double -> Double -> [Double] -> IO ()
rungekutta_44_s df h lim ps = rungekutta_44 (dfn ++ [df]) h lim ps
  where dfn = map dndt [0..(length ps - 3)]
        dndt n = (!! (n + 2))

簡単な方程式でテストしてみる。方程式や初期値はリストであたえているので、数や順番は自分で気をつけないといけない。ライブラリにする場合は別の方法を考えた方がいいかもしれない。

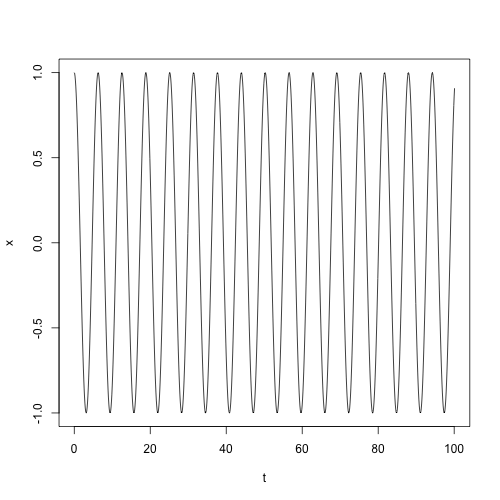
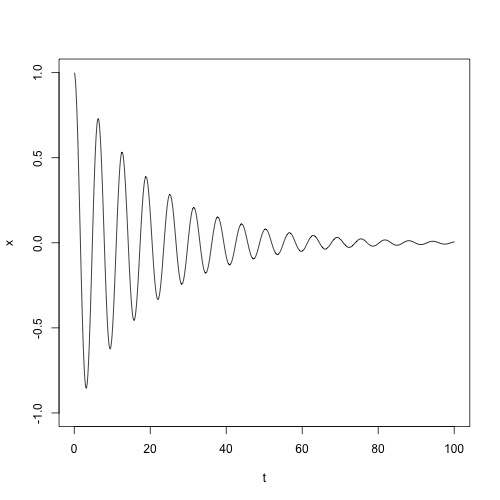
> -- 調和振動
> rungekutta_44 [\[t,x,v] -> v,\[t,x,v] -> -x] 0.1 100.0 [0.0,1.0,0.0]
> -- 減衰振動
> rungekutta_44_s (\[t,x,v] -> -x - 0.1*v) 0.1 100.0 [0.0,1.0,0.0]

もう少し面白いローレンツアトラクタなども描いてみる。

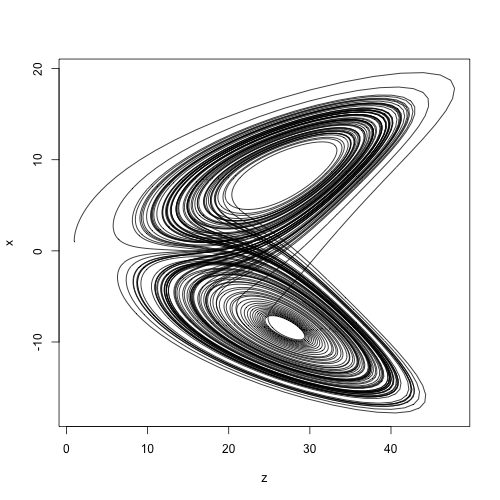
> let l_dxdt [t,x,y,z] = -10.0*x + 10.0*y
> let l_dydt [t,x,y,z] = -x*z + 28.0*x - y
> let l_dzdt [t,x,y,z] = x*y - 8.0/3.0 * z
> rungekutta_44 [l_dxdt,l_dydt,l_dzdt] 0.01 100.0 [0.0,1.0,1.0,1.0]

Newton-Raphson法

人間誰しも連立非線形方程式を解きたくなることがあるはずだ。Newton-Raphson法は微分係数を使って解に近づいていく収束が速いアルゴリズムで、適切な関数に対して適切な初期値をあたえれば、近くにある解を1つ見つけてくれる。ただ、収束しないこともあるし、自動的にすべての解を見つけてくれるわけではない。
まずは1変数の場合。微分係数は差分で近似している。deltaを小さくし過ぎると数値誤差で結果が悪化することもあるので注意が必要。数値微分で精度が必要な場合は中心差分や高階差分なども検討されたい。

delta = 1.0e-9 :: Double

derivative :: (Double -> Double) -> Double -> Double
derivative f x = (f (x + delta) - f x) / delta

newton :: Int -> Double -> (Double -> Double) -> Double -> Maybe Double
newton lim err f x
  | lim <= 0 = Nothing
  | abs fx < err = Just x
  | otherwise = newton (lim - 1) err f sx
  where sx = x - (fx / dfdx)
        fx = f x
        dfdx = derivative f x

簡単な関数でテストしてみる。発散したらすぐに打ち切るべきか。

> newton 1000 1.0e-9 (\x -> x^2 - 4.0) 4.0
=> Just 2.0000000000000053
> newton 1000 1.0e-9 (\x -> x^2 - 4.0) 0.0
=> Nothing

多変数の場合に拡張する。微分係数をJacobi行列 (偏微分係数を並べた行列) に置き換えて、関数とパラメータをベクトル化しただけで、ほとんど同じに書ける。速度が必要な場合はリストをData.Vector.UnboxedのVectorやData.Vector.Unboxed.MutableのMVectorに置き換えて、ランダムアクセスやin placeな書き換えも使うと良いかもしれない。

import qualified Numeric.LinearAlgebra as L

delta = 1.0e-9 :: Double

derivative_p :: ([Double] -> Double) -> [Double] -> [Double]
derivative_p f xs = zipWith dfdx xs [0..]
  where dfdx x i = (f (replace xs i (x + delta)) - f xs) / delta
        replace xs i x = let (l, _:r) = splitAt i xs in l ++ (x : r)

newton_m :: Int -> Double -> [[Double] -> Double] -> [Double] -> Maybe [Double]
newton_m lim err fs xs
  | lim <= 0 = Nothing
  | L.norm_2 fx < err = Just xs
  | otherwise = newton_m (lim - 1) err fs sx
  where sx = L.toList $ L.vector xs - (L.inv j L.#> fx)
        fx = L.vector $ map ($ xs) fs
        j = L.fromLists $ map (`derivative_p` xs) fs

適当な関数でテストしてみる。

> let vf0 [x,y,z,t] = 2.0*x^2 - y^3 + z - exp t
> let vf1 [x,y,z,t] = 3.0*x - 6.0*y^5 - 2.0*z*t
> let vf2 [x,y,z,t] = 2.0*x^2 - y - 2.0*z*t
> let vf3 [x,y,z,t] = x^4 + y*z - 2.0*t
> newton_m 1000 1.0e-9 [vf0,vf1,vf2,vf3] [1.0,2.0,3.0,4.0]
=> Just [1.066252215687592,0.7772738508955951,0.7861552762455988,0.9517927114657457]
> let a = [1.066252215687592,0.7772738508955951,0.7861552762455988,0.9517927114657457]
> map ($ a) [vf0,vf1,vf2,vf3]
=> [1.3322676295501878e-15,1.5543122344752192e-15,1.9984014443252818e-15,1.5543122344752192e-15]

Double程度の精度で解けていそうだ。適宜deltaやerrを調整する必要があるかもしれない。

Newton-Cotes型定積分

等間隔で関数値があたえられている時に積分値を計算する、Newton-Cotes型と呼ばれる一連のアルゴリズムがある。なかでも2次関数で補間するSimpson法はよく使われている気がする。4次関数で補間するBoole法もためしてみた。

newton_cotes :: [Double] -> Double -> (Double -> Double) -> Int -> Double -> Double -> Double
newton_cotes ces ce f n a b = ((b - a) / (r ^ n)) * ce * ig n a b
  where r = fromIntegral $ length ces - 1
        ig n a b
          | n == 1 = sum $ zipWith (*) (map f cs) ces
          | otherwise = sum $ zipWith (ig (n - 1)) cs (tail cs)
          where cs = map (\i -> a + i * ((b - a) / r)) [0.0..r]

simpson :: (Double -> Double) -> Int -> Double -> Double -> Double
simpson = newton_cotes [1.0,4.0,1.0] (1.0/3.0)

boole :: (Double -> Double) -> Int -> Double -> Double -> Double
boole = newton_cotes [7.0,32.0,12.0,32.0,7.0] (2.0/45.0)

分割位置のリスト生成について、数値誤差で長さが変わらないように冗長に見える方法をとってみた。簡単な関数でテストしてみる。

> simpson (\x -> x^4) 4 0.0 1.0
=> 0.20000203450520831
> boole (\x -> x^4) 2 0.0 1.0
=> 0.2

Boole法のほうが次数は高いが必ず精度が良いとは限らない。